728x90
반응형
Logistic Regression(로지스틱 회귀)
선형 회귀를 입력으로 받아 특정 레이블로 분류
- 독립 변수의 선형 결합을 이용하여 사건의 발생 가능성을 예측하는데 사용되는 통계 기법
- 선형 회귀 분석과는 다르게 종속 변수가 범주형 데이터를 대상으로 하며 입력 데이터가 주어졌을 때 해당 데이터의 결과가 특정 분류로 나뉘기 때문에 일종의 분류(classification) 기법으로도 볼 수 있음
- 이진 분류 문제(1과 0 중에 하나를 판별하는 문제)는 로지스틱 회귀를 이용하여 풀어 갈 수 있다
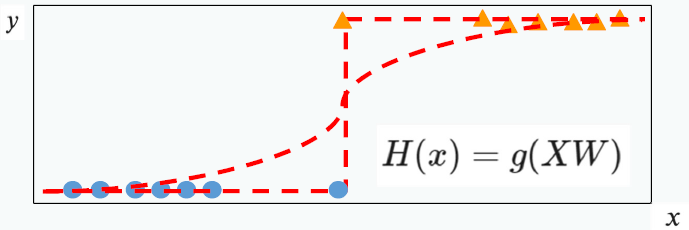



Sigmoid 함수도 w와 b를 구하는 것이 목적
| w 그래프의 경사도 값이 커지면 경사가 커지고, 값이 작아지면 경사가 작아짐 |
b 그래프의 좌우 이동을 의미 값이 크고 작아짐에 따라 그래프가 이동 |
 |
 |
Error, Cost or Loss Function
Logistic Regression에 Linear Regression에서 사용한 Loss Function MSE(Mean Square Error)를 적용할 경우 문제점

Non-Convex Function : Local Optimal에 빠질 수 있다.



미분하면 1과 0에 수렴하는 부분은 굉장히 작은 값으로 나타내져 학습이 잘 안되거나 느려짐
새로운 Cost Function or Loss Function 적용
- 시그모이드 함수의 특징을 보면 y값은 0 ~ 1사이 값이며 정답은 0 또는 1이다.
- Case 1) 실제 값이 1일 때 예측 값이 0에 가까워지면 오차가 커져야 한다
- Case 2) 실제 값이 0일 때 예측 값이 1에 가까워지면 오차가 커져야 한다
Cross Entropy (크로스 엔트로피)
- 서로 다른 두 확률 분포의 차이를 의미
- 로지스틱 회귀 관점에서는 모델의 예측값의 확률과 실제값 확률의 차이
- 예측값과 실제값의 차이를 가장 작제하는 w를 구함으로써 최적의 w를 구하는 방법

- y = -(y * log(hypothesis) + (1-y)log(1-hypothesis))
- 정답= 1: -log(hypothesis) 식 사용
- 정답= 0: -log(1-hypothesis)

Perceptron Summary
Linear Regression

문제점: Binary Classification에서 사용할 시 풀리지 않을 때가 존재함
Logistic Linear Regression (Sigmoid만 적용)

해결점: 출력할 때 Sigmoid 함수를 통해서 출력 0 ~ 1 사이 값이며 커브피팅 효과
문제점: 기존 MSE loss를 사용하면 두가지 문제점이 존재
- Local Min에 빠질 확률이 큼
- 시그모이드 미분값으로 w 학습이 잘 안되거나 느림
Logistic Regression (Classification)

해결점: MSE loss 함수 대신 Binary Cross Engropy loss 함수 적용
728x90
반응형
'Machine Learning > Supervised Learning' 카테고리의 다른 글
| [Supervised Learning][Classification] SVM(Support Vector Machine) (0) | 2021.03.24 |
|---|---|
| [Supervised Learning] Ensemble (0) | 2021.03.24 |
| [Supervised Learning] Decision Tree (0) | 2021.03.24 |
| [Supervised Learning][Regression] Linear Regression (0) | 2021.03.24 |
| [Supervised Learning][Classification] KNN(K-Nearest Neighbor) (0) | 2021.03.24 |