반응형
SVM(Support Vector Machine)
- 각 훈련 데이터 포인트들의 클래스 결정 경계(decision boundary)를 구분하는 것을 학습
- Support Vector: 두 클래스 사이의 경계에 위치한 데이터 포인터
- 새로운 데이터 포인트에 대해 예측할 때는 데이터 포인트와 각 서포트 벡터와의 거리를 측정
- 서로 다른 클래스를 지닌 데이터 사이의 간격이 최대가 되는 선이나 평면을 찾아 이를 기준으로 각 데이터를 분류하는 모델
- 데이터 사이에 존재하는 여백을 최대화, 일반화하여 성능을 극대화
Margin
- 서포트 벡터와 결정 경계 사이의 거리
- SVM의 목표는 마진을 최대로 하는 결정 경계를 찾는 것

- Decision boundary(결정 경계): 서로 다른 분류값을 결정하는 경계
- 데이터의 벡터 공간을 N차원이라고 할 때, 결정 경계 = N-1 차원
- Support Vector(서포트 벡터): 결정 경계를 만드는 데 영향을 주는 최전방 데이터 포인트
- Margin: 결정 경계와 서포트 벡터 사이의 거리
Kernel-SVM
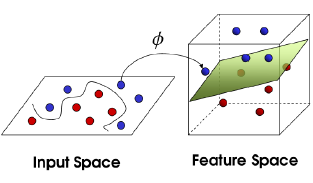
- 원공간(Input Space)의 데이터를 선형분류가 가능한 고차원 공간(Feature Space)으로 매핑한 후 두 범주를 분류하는 초 평면을 찾는 것
- 복잡한 형태의 데이터 셋에 비선형 특성을 추가하면 선형모델을 강력하게 만들 수 있지만 연산 비용이 커지는 문제가 발생
- 연상량이 폭증하는 이유는 모든 관측치에 대해 고차원으로 매핑하고 이를 다시 내적(inner product)를 해야 하기 때문
- 고차원 매핑과 내적(inner product)을 한번에 하기 위해 Kernel 도입
매핑 함수
- 저차원의 데이터를 고차원의 데이터로 옮겨주는 함수
- 매핑 함수를 가지고 실제로 많은 양의 데이터를 저차원에서 고차원으로 옮기기에는 계산량이 너무 많아서 현실적으로 사용하기 어려움
Kernel trick
- 실제로 데이터를 고차원으로 보내진 않지만 보낸 것과 동일한 효과를 줘서 매우 빠른 속도로 결정 경계선을 찾는 방법
선형 서포트 벡터 머신

다항 커널(Polynomial Kernel)

RBF(Radial Basis Function) 또는 가우시안 터널(Gaussian Kernel)
데이터포인트에 적용되는 가우시안 함수의 표준편차를 조정함으로써 결정 경계의 곡률을 조정

파라미터 튜닝
Gamma(γ)
커널의 표준편차의 조정 변수를 감마(gamma)라고 함
감마가 커지면 데이터포인트별로 허용하는 표준편차가 작아져서 결정 경계가 작아지면서 구부러짐
-> 작을수록 데이터포인트의 영향이 커져서 경계가 완만해지고, 클수록 데이터포인트가 결정 경계에 영향을 적게 미쳐 경계가 구부러진다.
- 가우시안 커널의 폭을 제어하는 매개 변수
- 가우시안 커널 폭의 역수에 해당
- 하나의 훈련 샘플이 미치는 영향의 범위를 결정
- 작은 값은 넓은 영역을 뜻하며 큰 값이라면 영향이 미치는 범위가 제한적
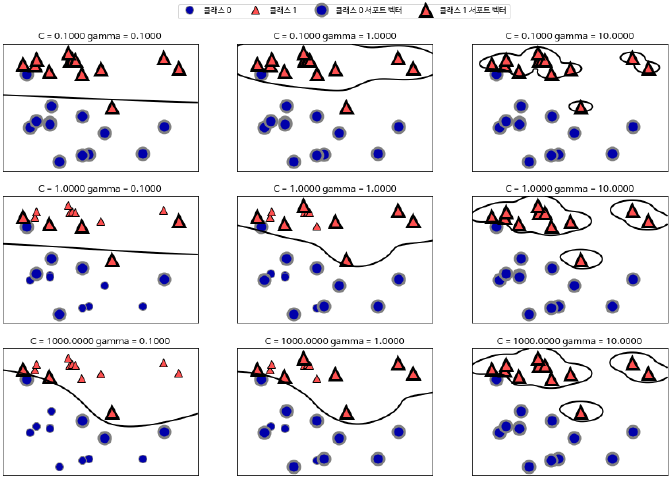
C (cost) 매개변수
마진 너비 조절 변수
클수록 마진 너비가 좁아지고, 작을수록 마진 너비가 넓어진다.
- 선형 모델에서 사용한 것과 비슷한 규제 매개 변수
- 포인트의 중요도를 제한
시그모이드 커널(Sigmoid Kernel)

SVM 장점과 단점
장점
커널 트릭을 사용함으로써 특성이 다양한 데이터를 분류하는 데 강하다
- N개의 특성을 가진 데이터는 N차원 공간의 데이터 포인트로 표현되고, N차원 공간 또는 그 이상의 공간에서 초평면(hyperplane)을 찾아 데이터 분류가 가능
파라미터(C, gamma)를 조정해서 overfitting 및 underfitting에 대처할 수 있다.
적은 학습 데이터로도 딥러닝만큼 정확도가 높은 분류를 기대할 수 있다.
단점
데이터 전처리 과정이 상당히 중요하다
- 특성이 비슷한 수치로 구성된 데이터의 경우에는 SVM을 쉽게 활용할 수 있지만 특성이 다양하거나 혹은 확연히 다른 경우에는 데이터 전처리 과정을 통해 데이터 특성 그대로 벡터 공간에 표현해야 한다.
특성이 많을 경우 결정 경계 및 데이터의 시각화가 어렵다
- 결정 경계를 시각화하기다 어려워 수학적 전문 지식없는 경우 분류 결과를 이해하기 어렵다
728x90
반응형
'Machine Learning > Supervised Learning' 카테고리의 다른 글
| [Supervised Learning][Classification] Naïve Bayes (0) | 2022.09.28 |
|---|---|
| [Supervised Learning][Regression] Ridge Regression, Lasso Regression (0) | 2022.09.27 |
| [Supervised Learning] Ensemble (0) | 2021.03.24 |
| [Supervised Learning] Decision Tree (0) | 2021.03.24 |
| [Supervised Learning][Regression] Linear Regression (0) | 2021.03.24 |