728x90
반응형
DBSCAN(Density-based Spatial Clustering of Application with Noise)
data의 분포가 세밀하게 몰려 있어서 밀도가 높은 부분을 중심으로 클러스터링을 하는 방식
어떠한 점을 기준으로 반경 ε 내에 점이 n개 이상 있으면 하나의 군집으로 인식
- 밀도 기반 클러스터링
- 비선형 클러스터의 군집이나 다양한 크기를 갖는 공간 데이터를 보다 효과적으로 군집하기 위해 이웃한 개체와의 밀도를 계산하여 군집하는 기법
- K-Means와 같이 군집 이전에 클러스터의 개수가 필요하지 않고 잡음에 대한 강인성이 높기 때문에 현재까지도 다양한 분야에서 활용
Algorithm
eps-neighbors와 minPts를 사용하여 군집을 구성
- Eps(ε) : 클러스터에 이웃을 포함할 수 있는 최대 반지름 거리
- Eps-neighbors: 한 데이터를 중심으로 epsilone 거리 이내의 데이터들을 한 군집으로 구성
- MinPts: 클러스터를 형성하기 위해 필요한 최소 이웃 수. 한 군집은 minPts 보다 많거나 같은 수의 데이터로 구성됨. 만약 minPts보다 적은 수의 데이터가 eps-neighbors를 형성하면 노이즈(noise)로 취급함


Core Vector(object)
- 임의의 벡터로부터 반경 Eps(ε)내에 있는 이웃 벡터의 수가 minPtsminPts보다 클 경우, 하나의 군집을 생성하며 중심이 되는 벡터
Border Vector(object)
- 핵심 벡터로부터 거리 Eps(ε)내에 위치해서 같은 군집으로 분류되나, 그 자체로는 핵심 벡터가 아닌, 군집의 외각에 위치하는 벡터
Noise Vector(object)
- 핵심 또는 외각 벡터가 아닌, 즉 Eps(ε)이내에 mitPtsmitPts개 미만의 백터가 있으며, 그 벡터들 모두 핵심 백터가 아닐 경우, 어떠한 군집에도 속하지 않는 벡터
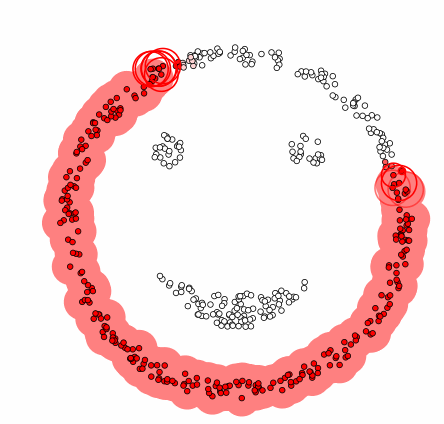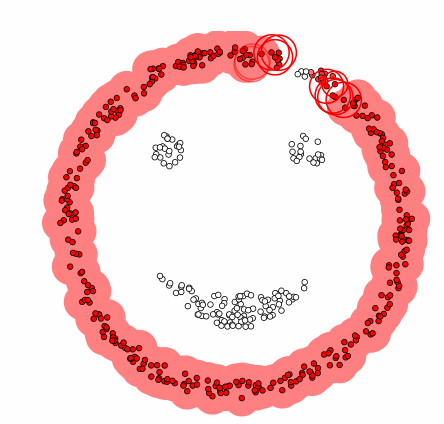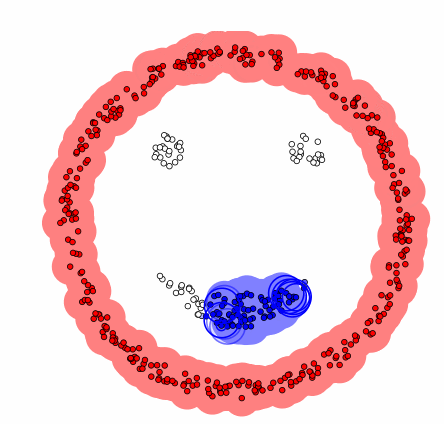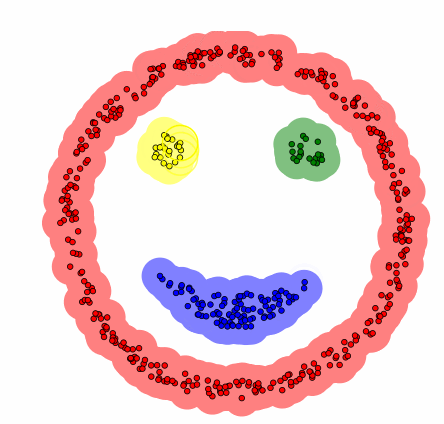
DBSCAN 모델 과정
Data를 군집하기 위한 반경(epsilon, ε)을 정의
반경 내에서 cluster와 outlier를 구분하기 위한 minpoinsts를 정의
- 무작위로 데이터 선택
- 선택된 데이터로부터 지정된 거리(epsilon, ε) 안의 모든 데이터(이웃) 탐색
- 이웃의 개수가 최소기준(minpoinsts)보다 많으면 (아닐 시 noise 처리) 클러스터 생성 후 이웃 확인
- 이웃이 클러스터에 할당되지 않았으면 해당 클러스터에 할당 후 이웃의 이웃을 탐색
- 클러스터 내의 모든 이웃에 대하여 더 이상 이웃이 없을 때까지 단계 4를 반복
- 한 번도 방문한 적 없는 데이터에 대하여 단계 1~4 반복
장점
K-means와 달리 초기 "K"값(클러스터의 개수)을 설정할 필요가 없다.
임의의 모양, 임의의 크기의 clustering이 가능하며, noise point를 고려한 clustering 또한 가능하다.
- 복잡한 모양에서도 구분할 수 있음
- 어떤 클래스에도 속하지 않은 포인트(noise)를 구분할 수 있음
- 큰 데이터셋에도 적용 가능
단점
agglomerative clustering이나 k-means 보다 느림
초기에 epsilon과 minpoins를 설정해야 한다.
data의 밀도가 다양한 경우에 적합하지 않다.
DBSCAN은 local density에 대한 정보를 반영해줄 수 없고, 또한 데이터들의 계층적 구조를 반영한 clustering이 불가능하다.
-> 이를 개선한 알고리즘: HDBSCAN(Hierarchical DBSCAN)
References
728x90
반응형
'Machine Learning > Unsupervised Learning' 카테고리의 다른 글
| [Unsupervised Learning] [Clustering] Agglomerative Clustering(병합 군집) (0) | 2022.10.05 |
|---|---|
| [Unsupervised Learning] Clustering (0) | 2022.10.05 |
| [Unsupervised Leaerning][Clustering] HDBSCAN(Hierarchical DBSCAN) (0) | 2022.10.05 |
| [Unsupervised Learning][Clustering] Mean Shift (평균 이동) (1) | 2022.10.05 |
| [Unsupervised Learning][Clustering] K-means (K 평균) (0) | 2022.10.04 |