728x90
반응형
Neural Network의 한계
- Vanishing Gradient
- Local Minima
- Overfitting
- 느린 학습
Vanishing Gradient
- Layer를 쌓아서 비선형 문제를 풀고 Backpropagation으로 multi layer를 학습하지만 전파하는 과정에서 기울기 값이 사라져 학습 안됨
- backpropagation은 출력층부터 앞으로 하나씩 되돌아가며 각 층의 가중치를 수정하는 방법 사용
- 가중치를 수정하려면 출력 오차 값(loss)을 미분하여 사용
- layer가 늘어나면 기울기가 중간에 0이 되어 버리는 기울기 소실(vanishing gradient) 문제가 발생
- activation 함수로 사용된 sigmoid 함수의 특성 때문에 발생
- sigmoid 미분하면 최대치가 0.3이 되고 layer를 거쳐갈수록 기울기가 사라져 가중치를 수정할 값이 소실됨

Vanishing Gradient Solution
- 문제를 해결하고자 여러 activation 함수가 만들어짐
- 비선형이면서 loss 전파를 잘되고(미분 값이 작으면) zero-centered한(optional 조건) 함수


sigmoid
비선형으로는 좋지만
- 문제 1) Gradient Vanishing 발생
- 문제 2) zero-centered (0점을 기준으로 대칭을 가짐)가 아니라서 학습을 불안정하게 만듦
- zero-centered가 아니면 w의 gradient가 한쪽으로 치우침(양수 또는 음수)
- 문제 3) exp의 연산 비용이 큼(연산이 어려움)
※ Layer가 깊지 않은 경우에는 간단히 사용 가능
tanh
- 문제 1) Gradient Vanishing 완전 삭제가 되지 않음
- 문제 2) exp의 연산 비용이 큼(연산이 어려움)
Relu
- 문제 1) zero-centered가 아님 ==> 하지만 학습은 잘됨
- 문제 2) 0 이하의 값은 전부 0으로 처리가 됨
leaky Relu
parametric Relu(PReLU)
Exponential Linear Units(ELU)
가중치 감소 기법 (xavier와 he 초기화)
Vanishing Gradient와 Local Minima를 해결 가능
weight를 잘 초기화 하자
- large random value: w가 너무 커서 오버슈팅(-1, 1에 포화)
- small random value: 초반에 layer는 잘 분포되나, layer가 깊어질수록 layer들의 분산이 0으로 수렴
- 가중치 매개변수의 값이 작아지도록 학습하는 방법
- 가중치를 작게 만들고 싶으면 초기값도 최대한 작은 값에서 시작하는 것이 가장 일반적 방법
- hidden layer 활성화 값의 분포를 관찰하면 중요한 정보를 얻을 수 있음

xavier initialization
- 자비에르 글로로트와 요수아 벤지오의 논문에서 권장하는 가중치 초기값
- 각 측의 활성화값들을 광범위하게 분포시킬 목적으로 노드 개수 n개를 이용하여 √1/n 분포를 사용
- sigmoid or Tanh에 효율적
- Relu activation에서는 잘 동작되지 않음

he initialization
- Relu의 경우에는 카이밍 히의 이름을 따서 만든 he 초기값을 사용
- 표준편차가 √2/n 정규분포 값 사용
## he 초기화 방법
x = tf.keras.layers.Dense(10, activation='sigmoid',
kernel_initializer=tf.keras.initializers.he_normal())(input_Layer)
## xavier 초기화 방법
x = tf.keras.layers.Dense(10, activation='sigmoid',
kernel_initializer=tf.keras.initializers.glorot_uniform())(x)
Local Minima
- Cost 값을 줄여가면서 학습을 하는 과정에서 모델을 업데이트하지만 Layer가 깊어질수록 비선형의 Cost 함수에서 가장 작은 Cost 값을 찾지 못함
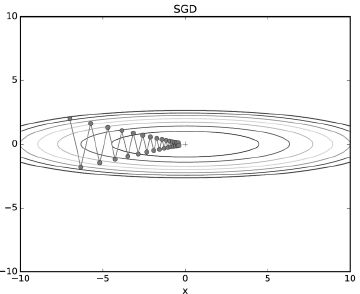
- 경사 하강법
- 학습 시 느린 학습 속도와 정확도 문제가 발생
- 정확하게 가중치를 찾아가지만, 한 번 업데이트할 때마다 전체 데이터를 미분해야 하므로 계산량이 매우 많다
- 비등방성 함수(방향에 따라 성질, 즉 기울기가 달라지는 함수)에서는 탐색 경로가 비 효율적
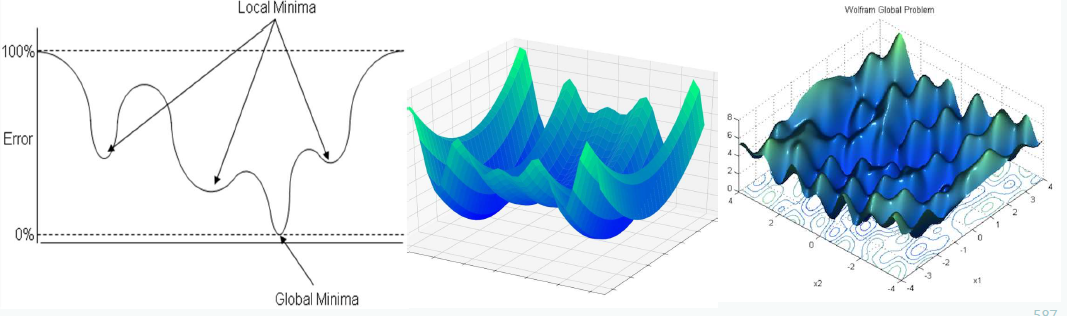
Local Minima Solution
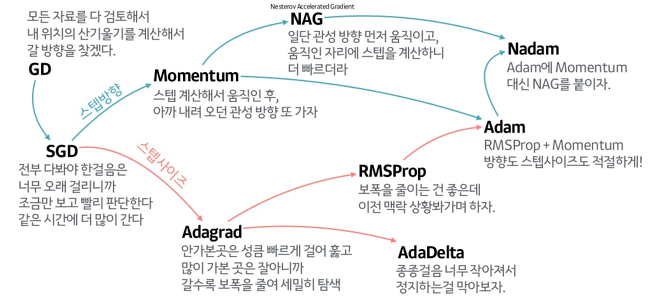
적절한 Optimizer를 선택하여 Local Minima, 느린 학습을 해결 가능!!
- 스텝 방향과 스텝 사이즈의 2가지 측면에서 적합한 optimizer가 존재
- Adam은 2가지 측면을 모두 고려하지만 모든 데이터에 적합한 것은 아님
- SGD, RMSProp, Adam이 가장 흔하게 쓰이는 optimizer
- SGD는 일반화를 고려할 때 사용하는 경우도 있음
Momentum
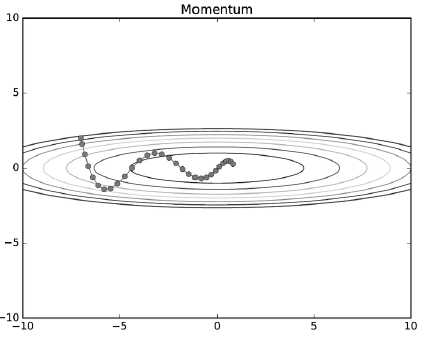
- 운동량을 뜻하는 단어로 물리와 관계가 있음
- 매번 기울기를 구하지만 이를 통한 오차를 수정하기 전 바로 앞 수정 값과 방향(+, -)을 참고하여 같은 방향으로 일정한 비율만 업데이트
- 전에 구해 놓은 미분값(오차 수정값)을 일부분 반영하여 현재의 미분값을 상충하는 효과가 있음
→ 빠른 속도로 학습이 가능
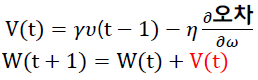
v = m * v -learning_rate * gradient
self.weight[i] += v
Nesterov Momentum
- 모멘텀을 개선해서 만든 알고리즘
- 모멘텀 방법으로 이동될 방향을 미리 예측하고 해당 방향으로 미리 이동한 gradient 값을 사용
- 속도는 그대로이면서 이동을 실행하기 전 한 단계를 미리 예측함으로써 불필요한 이동을 줄일 수 있음
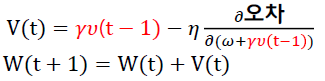
v = m * v -learning_rate * gradient(Self.weight[i-1] + m * v)
Self.weight[i] += v
Adagrad (Adaptive Gradient)

- 업데이트 수에 따라 학습률을 조절
- 최적 지점에 거의 도달할 경우 학습률을 조정함으로써 좀 더 세밀한 최적값을 얻을 수 있음
- G(t): t 스텝까지 각 스텝 별로 변수가 수정된 gradient 제곱을 모두 합한 값
- 𝜀: 아주 작은 상수. 0으로 나눈 것을 방지
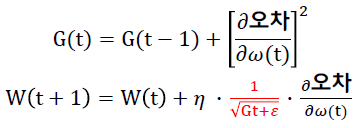
g += gradient ** 2
Self.weight[i] += -learning_rate * gradient / (np.sqrt(g) + e)
RMSprop
- Adagrad의 G(t) 값이 무한히 커지는 것을 방지하는 optimizer
- 이동 지수의 평균을 이용하여 G(t)값이 무한히 커지는 것을 방지
- 기울기의 영향을 억제하는 효과를 보이며 Adagrad의 G(t) 값에 해당하는 부분이 급격히 변하는 것을 방지
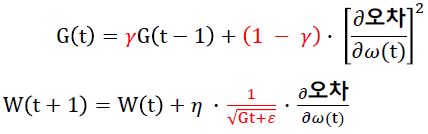
g = gamma*g + (1-gamma) * gradient ** 2
Self.weight[i] += -learning_rate * gradient / (np.sqrt(g) + e)
Adam
- RMSprop와 Momemtum 방식을 이용하여 업데이트한 optimizer
v = gamma1 * m + (1-gamma1) * dx
g = gamma2 * v + (1-gamma2) * (dx**2)
x += -learning_rate*g / (np.sqrt(v) + e)
Overfitting
- 다양한 Feature에 대해 과도하게 학습된 상황
- 학습할 때는 성능이 잘 나오지만 테스트 할 때는 성능이 나오지 않음
- train data에만 지나치게 적응되어 그 외의 데이터에서는 제대로 대응하지 못하는 상태
- High Variance, 과분산
- 비슷한 입력에 부정확 반응 결과가 나옴(학습대상만 정상 반응)
- Overfitting 발생 조건
- hidden layer가 너무 많거나 각 층의 노드 수가 많아 변수가 복잡해 질 경우
- test set과 train set이 중복될 때
- 모델링할 때 사용한 데이터가 전체 데이터에 대한 반영이 이루어지지 않은 경우(train 데이터가 적은 경우)
 |
 |
Underfitting
- 일부의 Feature에만 집중되어 학습된 상황
- 예측값이 실제값과 멀어져서 예측되어짐
- 데이터해석 능력 저하
- High bias, 과편향
- 여러 가지 입력에 제대로 반응 불가
- 새로운 데이터를 너무 잘 예측하는 상황(True=True로 예측, False=True로 오판 확률도 높음)
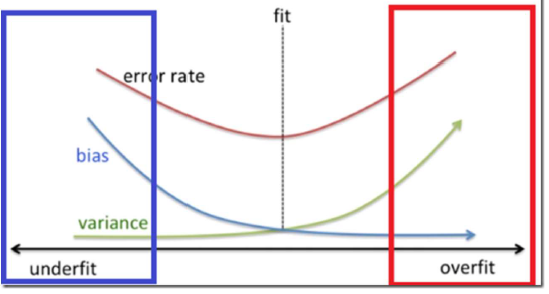
Overfitting / Underfitting 판단
Train/Validation/Test data의 loss 또는 Accuracy로 판단
→ 데이터의 의존성이 크다
현장/실제 상황에 가장 가까운 데이터를 많이 모아야 하고
데이터를 train/validation/test로 구분할 때 분포도가 잘 분배될 수 있도록 해야 한다.
Overfitting 방지 방법
학습 및 테스트 데이터셋 구분
- 모델링에 사용할 데이터셋을 학습 데이터셋과 테스트 데이터셋으로 구분해서 사용
- 학습 데이터와 테스트 데이터의 비율을 7:3이나 8:2 정도 사용
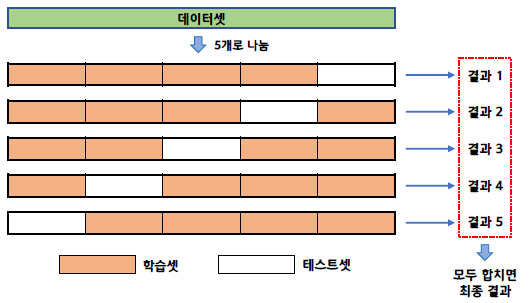
k겹 교차 검증
- 데이터 셋을 7:3 비율로 나눴다면 테스트셋은 겨우 전체 데이터의 30%만 사용하게 된다.
- 이 경우 30%의 테스트만으로 모델이 실제로 잘 작동하는지 확신하기는 쉽지 않다
↓
- 데이터셋을 여러 개로 나누어 하나씩 테스트셋으로 사용하고 나머지를 모두 합해서 학습셋으로 사용하는 방법
- 데이터의 100%를 테스트셋으로 사용할 수 있다.
Early Stopping
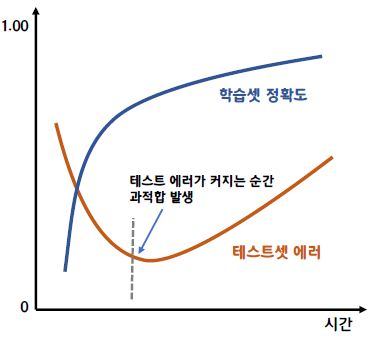
- 오버피팅 현상 발생 시 조기 학습 종료
- 학습데이터와 검증용 데이터로 나눠서 학습 시 학습 현황을 관찰하여 오버피팅 현상 일어날 경우 조기에 학습 종료
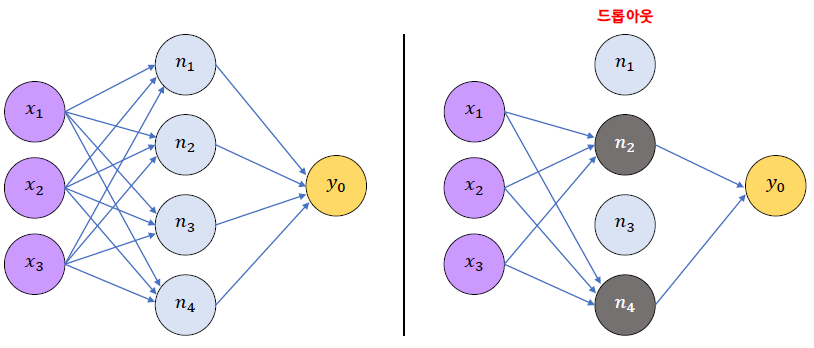
Dropout 규제 방법 사용
- 제프리 힌튼이 2012년에 제안
- 매 학습 단계에서 각 노드를 일정 비율로 학습에서 무시하는 것
- 매 epoch마다 일정 비율로 perceptron를 제외하고 학습
Data Augmentation (데이터 증식)
- 모든 데이터를 전부 수집하는 것은 현실적으로 불가능하기 때문에 실제와 같은 훈련 데이터를 생성하는 것
- 사람이 인공적으로 만든 샘플인지 구분할 수 없어야 함
- white noise를 추가하는 것은 도움이 되지 않음-> 적용한 수정사항이 학습 가능한 것이어야 함
- 이미지 데이터 증식할 때 유용
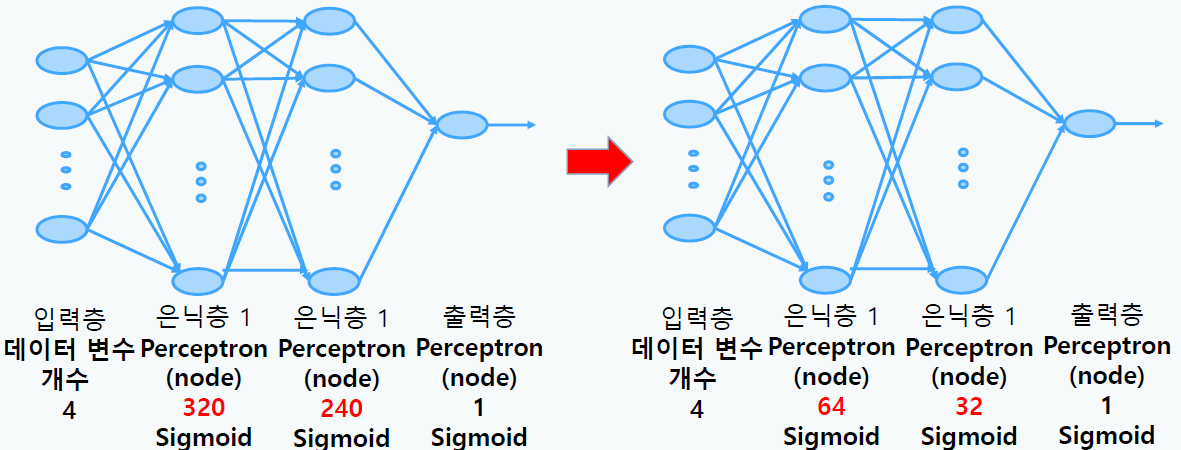
Shallow Learning(모델 간소화)
- Hidden layer와 Perceptron(node)를 간소화하여 모델링
Batch Nomalization
- 학습을 제대로 안정적으로 빠르게 진행시키기 위해 고려되었으나 추가적으로 Overfitting 감소 효과도 있음
- Layer와 Layer 사이에 Normalization을 추가
- 각각의 스칼라 Feature들을 독립적으로 정규화 하는 방식으로 진행
- 각각의 Feature들의 Mean 및 Variance를 0과 1로 정규화 하는 것
- Deep Neural Network 의 Internal covariate shift를 피하자
Internal Covariate Shift
- train data를 가지고 학습 할 때, 이전 레이어의 값이 다음 레이어에 값을 전달하는 형태이므로 결국 이전 레이어의 값 따라 다음 레이어의 가중치 값에 영향을 미침
- 아무런 규제 없이 가중치들이 학습하다보면 모델 파라미터가 제멋대로 범위가 넓어지거나 퍼지게 되어 있음. 또한 모델 파라미터 값들의 변동이 심해지는데 현상을 말함
Batch Nomalization 연산
- 각각의 스칼라 Feature들을 독립적으로 정규화 하는 방식으로 진행
- 각각의 Feature들의 Mean 및 Variance를 0과 1로 정규화 하는 것

입력받은 모든 값들의 평균을 구한다
B는 batch를 의미하므로 μB는 Batch 사이즈만큼의 feature들의 평균을 의미
구한 평균을 기반으로 입력받은 모든 값들의 분산을 구함
구한 평균과 분산을 기반으로 0~1사이로 정규화를 시킴
0~1의 정규화를 시키면 역전파알고리즘 효과를 줄임
→ 문제를 해결하기 위해 scale과 shift 적용
γ와 β를 통해 nomalize된 값을 scale과 shift를 해주는데
이 값을 학습을 통해 찾게되는 이는 결국 representation power를 유지해주는 역할
Benefits of BN
- Increase learning rate
- Remove dropout
- Reduce L2 weight decay
- Accelerate learning rate decay
- Remove local response normalization
Regularization
기타 방법
- Parameter Norm Penalties
- Dataset Augmentation
- Noise Robustness: to input, weights, and output
- Semi-Supervised Learning = learning a representation
- Multitask learning
- Parameter Tying and Parameter Sharing
- Sparse representation
- Bagging and Other Ensemble Methods
- Adversarial Training
Summary
Netrual Network 한계 대표 해결법
- Batch Normalization
- Dropout
- Regulation
- Small Model
- Data Augmentation
- 새로운 Activation 함수
- 최적의 Optimizer
학습 시 중요한 것
- 데이터를 모을 때 실제 현장과 비슷하거나 발생할 모든 케이스의 데이터를 많이 모아야 함
- 학습/검증/시험 데이터를 나눠서 학습 시 성능 확인을 하고 overfitting 확인 해야 함
- 데이터를 나눌 때 분포가 고르게 되어야 함
- 학습 모델 weight가 고루 잘 퍼져 있는게 일반적으로 잘 학습되었다고 할 수 있음
- 최적의 learning rate, 모델 파라미터 초기값, 모델 설계, batch size, ecoch 등을 검증해야 함
- 검증 데이터는 학습 시 모델 업데이트에 적용되지 않아야 함
References
728x90
반응형
'Machine Learning > Deep Learning' 카테고리의 다른 글
| epoch, batch size, iteration (0) | 2022.12.08 |
|---|---|
| [Machine Learning] Neural Network (0) | 2021.03.03 |
| [Machine Learning] Perceptron (0) | 2021.02.27 |