728x90
반응형
ufunc (Universal Function)
- ndarray 안에 있는 데이터 원소 별로 연산을 수행하는 함수
- 하나 이상의 스칼라 값을 받아서 하나 이상의 스칼라 결과 값을 반환하는 간단한 함수를 고속으로 수행할 수 있는 벡터화된 래퍼 함수
| 연산 | 함수 |
| 사칙연산 | add(), multiply(), negative(), exp(), log(), sqrt() |
| 삼각 함수 | sin(), cos(), hypot() |
| 비트 단위 | bitwise_and(), left_shift() |
| 관계형, 논리 | less(), logical_not(), equal() |
| 최대/최소 | maximum(), minimum(), modf() |
| 부동소수점에 적용 함수 | isinf(), infinite(), floor(), isnan() |
단항 유니버셜 함수
| 함수 | 설명 |
| abs, fabs | 각 원소의 절대값. 복소수가 아닌 경우 fabs를 쓰면 빠른 연산이 가능 |
| sqrt | 각 원소의 제곱근 계산 (arr**0.5) |
| square | 각 원소의 제곱율 계산 (arr**2) |
| exp | 각 원소의 지수 e^x 계산 |
| log, log10, log2, log1p | 자연로그, 밑 10인 로그, 밑 2인 록, log(1+x) |
| sign | 각 원소의 부호 (양수 1, 0, 음수 -1) |
| ceil | 각 원소의 값보다 같거나 큰 정수 중 가장 작은 값 |
| floor | 각 원소의 값보가 같거나 작은 정수 중 가장 큰 값 |
| rint | 각 원소의 소수자리를 반올림 |
| modf | 각 원소의 몫과 나머지를 각각의 배열로 반환 |
| isnan | 각 원소가 NaN인지 아닌지 불리언 배열로 반환 |
| isfinite, isinf | 각 원소가 유한한지 무한한지 불리언 배열로 반환 |
| cos, cosh, sin, sinh, tan, tanh | 일반 삼각함수, 쌍곡삼각함수 |
| arccos, arccosh, arcsin, arcsinh, arctan, artanh | 역삼각함수 |
이항 유니버셜 함수
| 함수 | 설명 | |
| add | + | 두 배열의 같은 위치의 원소끼리 더하기 |
| subtract | - | 첫 번째 배열의 원소에서 두 번째 배열의 원소를 뺌 |
| multiply | * | 같은 위치의 원소끼리 곱하기 |
| divide, floor_divide | /, // | 첫 번째 배열의 원소를 두 번재 배열의 원소로 나눔. floor는 몫만 취함 |
| power | ** | 첫 번째 배열의 원소를 두 번째 배열의 원소만큼 제곱함 |
| maximum, fmax | 각 배열의 두 원소 중 큰 값을 반환. fmax는 NaN 무시 | |
| minimum, fmin | 각 배열의 원소 중 작은 값을 반환. fmin는 NaN 무시 | |
| mod | % | 첫 번째 배열의 원소를 두 번째 배열의 원소로 나눈 나머지 |
| copysign | 첫 번째 배열의 원소의 기호를 두 번째 배열의 원소의 기호로 바꿈 | |
| greater, greater_equal, less, less_equal | 각 두 원소 간의 비교 연산(<, <=, >, >=, ==, !=)를 불리언 배열로 반환 |
where 함수
- np.where(조건, x, y): 'x if 조건 else y' 같은 삼학식의 벡터화 버전
- numpy를 사용하여 큰 배열을 빠르게 처리 가능하며, 다차원 배열도 간경하게 표현 가능
- 임의로 생성된 데이터의 특정 값을 원하는 값으로 바꿀 수 있다
arr = np.random.randn(4, 4)
arr
>>
array([[-0.94055232, -1.00650323, -1.18096948, -1.83203106],
[-0.47103769, -2.53258752, 0.16705334, -1.84778239],
[-0.04325452, 0.33106234, 0.83938198, 0.95471975],
[ 1.33032793, -1.33230257, -1.46370295, 0.02788888]])
np.where(arr > 0, 2, -2)
>>
array([[ 2, -2, 2, -2],
[ 2, 2, -2, 2],
[ 2, -2, 2, 2],
[-2, -2, -2, 2]])
any(), all()
- any(): 하나 이상의 값이 True이면 True 반환
- all(): 모든 값이 True이면 True 반환
import numpy as np
xarr = np.array([1.1,1.2,1.3,1.4,1.5])
yarr = np.array([2.1,2.2,2.3,2.4,2.5])
cond = np.array([True, False, True, True, False])
result = [(x if c else y) for x,y,c in zip(xarr, yarr, cond)]
print('result:', result)
result2 = np.where(cond, xarr, yarr)
print('result2:', result2)
>>
result: [1.1, 2.2, 1.3, 1.4, 2.5]
result2: [1.1 2.2 1.3 1.4 2.5]
수학 및 통계 메서드(Aggregate Function)
- 배열 전체 혹은 배열에서 한 축을 따르는 자료에 대한 통계를 계산하는 함수
- sum, mean 등의 함수는 axis를 인자로 받아서 해당 axis에 대한 통계를 계산 가능
- 축을 지정하지 않을 경우 배열 전체 대한 값을 연산
- 2차원 배열 기준
- axis=None: 전체 배열을 하나의 배열로 간주하고 집계 함수의 범위를 전체 행렬로 정의
- axis=0: 행을 기준으로 각 행의 동일 인덱스의 요소를 그룹으로 하고 이를 집계 함수의 범위로 정의
- axis=1: 열을 기준으로 각 열의 요소를 그룹으로 하고 이를 집계 함수의 범위로 정의
| 함수 | 설명 |
| sum(), mean() | 배열 전체 합, 평균 |
| cumsum(), cumprod() | 누적 합, 누적 곱 |
| std(), var() | 표준편차, 분산 |
| min(), max() | 최소값, 최대값 |
| argmin(), argmax() | 최소 원소의 색인 값, 최대 원소의 색인 값 |

import numpy as np
arr = np.random.randn(200, 500)
arr.shape
>>
(200, 500)
arr.sum()
np.sum(arr)
>>
371.4563054971811
arr.mean(axis=0).shape
>> (500,)
arr.mean(axis=1).shape
>> (200,)
불리언 배열을 위한 메서드
- numpy는 불리언 값을 이용한 배열의 값을 선택하고 처리할 수 있는 함수를 제공
- any, all 메서드는 불리언 배열에 사용할 때 유용
- any 메서드는 하나 이상의 True 값이 있는지 검사하고, all 메서드는 모든 원소가 True인지 검사할 때 사용
arr = np.random.randn(100)
(arr > 0).sum()
정렬
arr.sort()
- 파이썬의 내장 리스트형처럼 numpy에서도 sort 메서드를 이용하여 정렬 가능
- 주어진 축에 따라 정렬하며, 다양한 정렬방법들을 지원
- arr 자체를 정렬함(in-place)
np.random.seed(10)
arr = np.random.randint(1, 100, size=10)
arr
>> array([10, 16, 65, 29, 90, 94, 30, 9, 74, 1])
arr.sort()
arr
>> array([ 1, 9, 10, 16, 29, 30, 65, 74, 90, 94])
import numpy as np
arr = np.random.randn(3, 3)
arr
>>
array([[ 2.30765072, -0.1339542 , -0.14067305],
[ 1.22580775, 2.02457619, -0.02324537],
[-1.29122669, 0.84210548, -2.05418146]])
arr.sort(axis = 1)
arr
>>
array([[-0.14067305, -0.1339542 , 2.30765072],
[-0.02324537, 1.22580775, 2.02457619],
[-2.05418146, -1.29122669, 0.84210548]])
arr.sort(axis = 0)
arr
>>
array([[-2.05418146, -1.29122669, 0.84210548],
[-0.14067305, -0.1339542 , 2.02457619],
[-0.02324537, 1.22580775, 2.30765072]])
np.sort(arr, axis=-1)
- np.sort는 배열을 직접 변경하지 않고 정렬된 결과를 가진 복사본을 반환
np.random.seed(20)
arr = np.random.randint(1, 100, size=10)
arr
>>
array([91, 16, 96, 29, 91, 10, 21, 76, 23, 72])
np.sort(arr)
>>
array([10, 16, 21, 23, 29, 72, 76, 91, 91, 96])
-np.sort(-arr)
>>
array([96, 91, 91, 76, 72, 29, 23, 21, 16, 10])
집합 함수
1차원 ndarray를 위한 집합 연산을 제공
| 함수 | 설명 |
| unique(x) | 배열 x에서 중복된 원소를 제거한 후 정렬하여 반환 |
| intersect1d(x, y) | 배열 x와 y에 공통적으로 존재하는 원소를 정렬하여 반환 |
| union1d(x, y) | 두 배열의 합집합을 반환 |
| in1d(x, y) | x의 원소 중 y의 원소를 포함하는지를 나타내는 불리언 배열을 반환 |
| setdiff1d(x, y) | x와 y의 차집합을 반환 |
| setxor1d(x, y) | 한 배열에는 포함되지만 두 배열 모두에는 포함되지 않는 원소들의 집합인 대칭차집합을 반환 |
선형대수
- 행렬의 곱셈, 분할, 행렬식과 같은 선형 대수에 관한 함수 제공
| 함수 |
설명 |
| numpy.dot(a, b) | 행렬 곱셈. 벡터의 내적 |
| numpy.diag | 정사각 행렬의 대각/비대각 원소를 1차원 배열로 반환하거나, 1차원 배열을 대각선 원소로 하고 나머지는 0으로 채운 단위 행렬을 반환 |
| numpy.trace | 행렬의 대각선 원소의 합을 계산 |
| numpy.linalg.det | 행렬식을 계산(ad-bc) |
| numpy.linalg.eig | 정사각 행렬의 고유 값과 고유 벡터를 계산 |
| numpy.linalg.inv | 정사각 행렬의 역행렬을 계산 |
| numpy.linalg.solve | A가 정사각 행렬일 때 Ax = b를 만족하는 x를 구함 |
| numpy.linalg.lstsq | y = xb를 만족하는 최소제곱해를 구함 |
| numpy.linalg.svd | 특이값 분해(SVD)를 계산 |
np.dot(a, b)
- 2개의 2차원 배열을 * 연산자로 곱하는 건 행렬 곱셈이 아니라 대응하는 각 원소의 곱을 계산하는 것
- 행렬 곱셈은 배열 method이자 numpy 네임스페이스 안에 있는 함수인 dot 함수를 사용해서 계산
- array@array
- 행렬곱 수행 시, 앞의 배열에 대하여 열의 길이가 뒤의 배열에 대하여 행의 길이와 같지 않으면 오류 발생
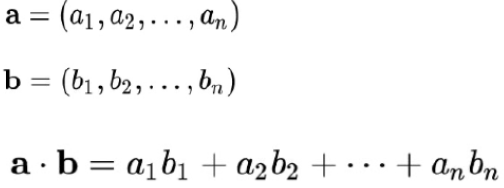
import numpy as np
x = np.array([[1,2,3],[4,5,6]])
y = np.array([[6,23],[1,-7],[8,9]])
print(x.dot(y))
>>
[[ 32 36]
[ 77 111]]
np.matmul(a, b)
- matrix multiplication. 행렬의 곱
- matmul을 수행할 시 shape를 유의
- shape가 맞지 않는 경우 ValueError 발생
- 3차원 이상의 경우 마지막 2개의 축으로 이루어진 행렬을 다른 축들에 따라 쌓은 것으로 파악
- 마지막 2개의 차원이 행렬곱이 가능하다면 matmul 가능

a = np.random.randint(-3, 3, 10).reshape(2, 5)
b = np.random.randint(0, 5, 15).reshape(5, 3)
a.shape, b.shape
>>
((2, 5), (5, 3))
ab = np.matmul(a, b)
print(ab.shape)
print(ab)
>>
(2, 3)
[[ -3 -15 -15]
[ -9 -6 1]]
a = np.arange(24).reshape(2, 3, 4)
b = np.arange(2*4*5).reshape(2, 4, 5)
a
>>
array([[[ 0, 1, 2, 3],
[ 4, 5, 6, 7],
[ 8, 9, 10, 11]],
[[12, 13, 14, 15],
[16, 17, 18, 19],
[20, 21, 22, 23]]])
b
>>
array([[[ 0, 1, 2, 3, 4],
[ 5, 6, 7, 8, 9],
[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]],
[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29],
[30, 31, 32, 33, 34],
[35, 36, 37, 38, 39]]])
a.shape, b.shape
>>
((2, 3, 4), (2, 4, 5))
arr = np.matmul(a, b)
arr
>>
array([[[ 70, 76, 82, 88, 94],
[ 190, 212, 234, 256, 278],
[ 310, 348, 386, 424, 462]],
[[1510, 1564, 1618, 1672, 1726],
[1950, 2020, 2090, 2160, 2230],
[2390, 2476, 2562, 2648, 2734]]])
arr.shape
>>
(2, 3, 5)
난수 생성
numpy.random 모듈
- 다양한 종류의 확률분포로부터 효과적으로 표본값을 생성
- 파이썬 내장 random 모듈에 비해 더 효율적으로 값을 생성하여 파이썬 내장 모듈보다 수십 배 이상 빠른 속도
| 함수 | 설명 |
| seed | 난수 생성기의 seed를 지정 난수 발생을 위한 seed를 고정하여 reproduction 시 활용 |
| permutation | 순서를 임의로 바꾸거나 임의의 순열을 반환 |
| shuffle | 리스트나 배열의 순서를 뒤섞음 |
| rand | (0, 1) 범위의 균등분포에서 표본을 추출 |
| randint | 주어진 최소/최대 범위 내에서 임의의 난수 추출 |
| randn | 표준편차 1, 평균 0인 정규분포에서의 표본 추출 |
| binomial | 이항분포에서 표본 추출 |
| normal | 정규분포(가우시안)에서 표본 추출 |
| beta | 베타분포에서 표본 추출 |
| chisquare | 카이제곱 분포에서 표본 추출 |
| gamma | 감마분포에서 표본 추출 |
| uniform | 균등(0, 1)에서 표본 추출 |
728x90
반응형
'Python > Numpy' 카테고리의 다른 글
| [Numpy] Numpy Shape Manipulation (0) | 2021.03.05 |
|---|---|
| [Numpy] Numpy Vectorization & Broadcasting (0) | 2021.03.05 |
| [Numpy] Numpy (Numerical Python) (0) | 2021.02.24 |