Loss Function (손실 함수) / Cost Function (비용함수)
통계학, 경제학 등에서 널리 쓰이는 함수로 머신러닝에서도 손실함수는 예측값과 실제값에 대한 오차를 줄이는 데에 유용하게 사용
측정한 데이터를 토대로 산출한 모델의 출력값(예측값)과 정답(실제값)의 오차를 정의하는 함수
신경망을 학습할 때, 학습이 잘 되고 있는지 평가하는 하나의 지표로 사용
Cross-Entropy 라고도 한다.
손실함수(Loss Function): 한 개의 데이터 포인트에서 나온 오차를 최소화하기 위해 정의되는 함수
비용함수(Cost Function): 모든 오차를 일반적으로 최소화하기 위해 정의되는 함수
목적함수(Objective Function): 어떠한 값을 최대화 혹은 최소화 시키기 위해 정의되는 함수
Regression model Loss Function
[Regression Loss Function] MAE, MSE, RMSE MSLE, RMSLE
Information Theory (섀년의 정보이론)
- 정보량↑ = 빈번하지 않은 정보 = 불확실성↑
- 전체 메시지에서 잦은 단어는 정보량이 적고, 드문 단어는 정보량이 많다
Entropy
불확실성의 척도
물리학에서 분자들의 무질서도 혹은 에너지의 분산 정도를 나타내는 용어인데 정보학에서는 정보의 양으로서 신호를 인식하는 데 쓰인다.
엔트로피가 높다는 것은 정보가 많고, 확률이 낮다는 것을 의미

엔트로피가 정보학에서 쓰이게 되면 정보량의 기댓값(평균)을 의미
어떤 확률분포로 일어나는 사건을 표현하는 데에 필요한 정보량을 의미
확률분포의 무질서도나 불확실성, 혹은 정보 표현의 부담 정도를 나타내는 것
정보는 신호에 존재하는 정보의 양으로 비교할 수 있는데 정보의 양은 누구나 알만한 정보가 아닌 새롭고 특이해서 사람들을 놀라게 만드는 정보다 클 수록 많다라고 볼 수 있다.
P(x)는 x라는 사건이 발생할 확률, I(x)는 x의 정보량을 의미한다고 한다면 아래와 같은 특성을 가지고 있다.
- 불확실성이 클수록 정보의 양은 크다. 이라면
- 두 개의 별개의 정보량은 각 정보량의 합과 같다.
두 개의 독립적인 사건의 발생확률은 로 표현되는데 정보량은 합산이기 때문에 이를 만족시키기 위해 log를 씌워주어 주는 것이다. 즉, 가 된다. - 정보량은 bit로 표현된다.
Cross Entropy (교차 엔트로피)
정보 엔트로피는 하나의 확률분포가 갖는 불확실성(놀람의 정도) 혹은 정보량을 정량적으로 계산할 수 있도록 하는 개념
크로스 엔트로피는 두 가지 확률 분포가 얼마나 비슷한지를 수리적으로 나타내는 개념

실제 분포 q에 대해서 알지 못하는 상태에서 모델링을 통해 구한 분포인 p를 통해 q를 예측하는 것
q와 p가 모두 들어가기 때문에 크로스 엔트로피라고 부른다
- q: 딥러닝 모델의 추정 확률분포
- p: 딥러닝 모델이 추구해야 할 미지의 확률분포
q와 p를 활용하여 크로스 엔트로피를 계산하여 이 크로스 엔트로피가 낮아지는 쪽으로 모델의 추정 확률분포 q를 꾸준히 개선하여 확률분포 q를 p에 가깝게 접근시켜 나갈 수 있다.
크로스엔트로피에서는 실제값과 예측값이 맞는 경우에는 0으로 수렴하고 값이 틀린 경우에는 값이 커지기 때문에
두 확률분포가 서로 얼마나 다른지를 나타내주는 정량적인 지표 역할을 한다.
Log Loss
cross entropy는 log loss로 불리기도 한다
cross entropy를 최소화하는 것은 log likehood를 최대화하는 것과 같기 때문
전체 훈련 세트에 대한 비용 함수는 모든 훈련 샘플의 비용을 평균한 값
- 모델 성능 평가 시 사용 가능한 지표
- 분류(classification) 모델 평가 시 사용

최종적으로 맞춘 결과만 가지고 성능을 평가할 경우, 얼만큼의 확률로 해당 답을 얻은 건지 평가가 불가능하다.
이를 보완하기 위해 확률 값을 평가 지표로 사용
Log loss는 모델이 예측한 확률 값을 직접적으로 반영하여 평가
확률 값을 음의 log 함수에 넣어 변환을 시킨 값으로 평가하는데, 이는 잘못 예측할 수록 패널티를 부여하기 위함이다.
Classification model Loss Function
- Binary cross-entropy
- Categorical cross-entropy
Binary cross-entropy
binary classification를 훈련한다면 binary crossentropy 손실함수를 사용하는 것이 적절
이진 분류기는 true/false, 양성/음성처럼 2개의 클래스로 분류할 수 있는 분류기를 의미

손실함수는 예측값과 실제값이 같으면 0이 되는 특성을 갖고 있어야 한다.
이진분류기의 경우 예측값이 0과 1 사이의 확률값으로 나온다.
→ 0에 가까울수록, 1에 가까울수록 둘 중 한 클래스에 가깝다는 것
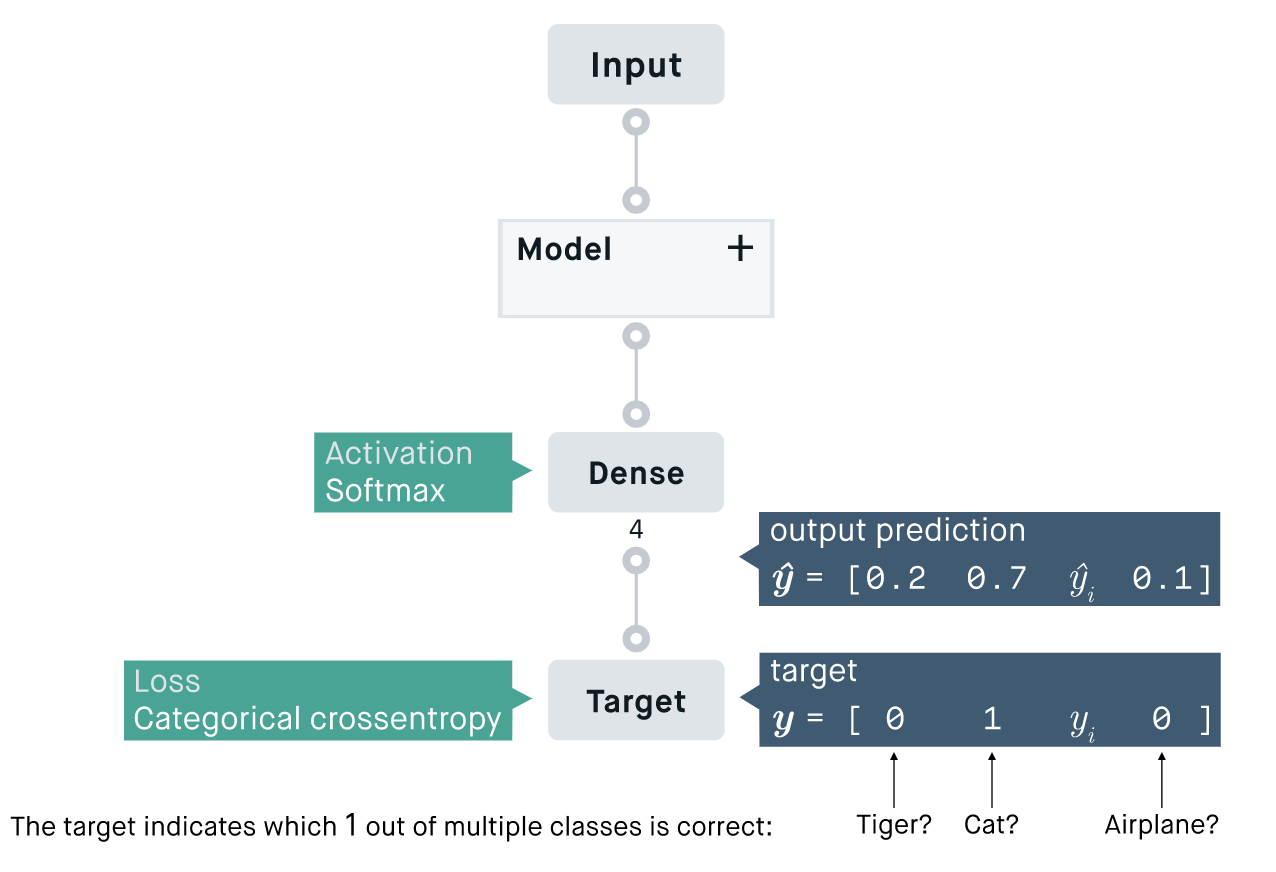
Categorical cross-entropy


Categorical cross-entropy는 분류해야할 클래스가 3개 이상(multi class classification)인 경우에 사용
softmax 활성함수와 함께 쓰이는 경우가 많아 softmax acitivation function이라고도 불린다.
Sparse Categorical cross-entropy
분류해야할 클래스가 3개 이상이며 라벨이 0, 1, 2처럼 정수의 형태로 제공될 때 주로 사용
References
- https://89douner.tistory.com/28
- https://velog.io/@yuns_u/손실함수-간략-정리
- https://seoyoungh.github.io/machine-learning/ml-logloss/
'Machine Learning > Machine Learning' 카테고리의 다른 글
| Machine Learning Valuation Metrics (머신러닝 모델 성능 평가) (0) | 2022.10.06 |
|---|---|
| [Machine Learning][Regression Loss Function] MAE, MSE, RMSE MSLE, RMSLE (1) | 2022.10.05 |
| Data Mining (데이터 마이닝) (1) | 2022.10.05 |
| [Machine Learning][Model Performance Measure] Precision, Recall, Accuracy, F1 score, FPR, ROC curve, AUC (0) | 2022.09.27 |
| [Machine Learning] 차원축소 (Dimensionality Reduction) (0) | 2021.05.12 |